人理解迭代神理解递归

                                                                                                                                递归要和迭代比较来看。

     迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值，因此迭代是从前往后计算的。

     递归则是一步一步往前递推，直到递归基础，寻找一条路径，然后再由前向后计算。

     迭代是从前往后计算的，而递归则是先从后往前推，然后再由前往后计算，有“递”又有“归”。

     递归经典案例还有斐波那契数列、?阶阶乘等，想要更好地掌握这个知识点，可以去免费试听《递归四讲》哦~

     戳我试听递归神解哦

     通俗来讲：

     一个小朋友坐在第 10 排，他的作业本被小组长扔到了第 1 排，小朋友要拿回他的作业本，可以怎么办？

     他可以拍拍第 9 排小朋友，说“帮我拿第 1 排的本子”，而第 9 排的小朋友可以拍拍第 8 排小朋友，说“帮我拿第 1 排的本子”…如此下去，消息终于传到了第 1 排小朋友那里，于是他把本子递给第 2 排，第 2 排又递给第 3 排…终于，本子到手啦！

     这就是递归，拍拍小朋友的背可以类比函数调用，而小朋友们都记得要传消息、送本子，是因为他们有记忆力，这可以类比栈。

     更严谨一些，递归蕴含的思想其实是数学归纳法：为了求解问题 p （ n ），首先解决基础情形 p （ 1 ），然后假定 p （ n-1 ）已经解决，在此基础上若 p （ n ）得解，那所有问题均得解。

递归三要素

     递归的定义：接受什么参数，返回什么值，代表什么意思。当函数直接或者间接调???时，则发?了递归

     递归的拆解：每次递归都是为了让问题规模变?

     递归的出?：必须有?个明确的结束条件。因为递归就是有“递”有“归”，所以必须又有一个明确的点，到了这个点，就不用“递下去”，而是开始“归来”。

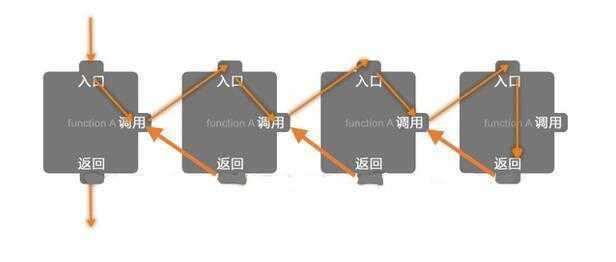
     点击在新窗口中浏览原图
CTRL+鼠标滚轮放大或缩小

下面这个求 n! 的例子中，递归出口（确定递归什么时候结束）是 fun(1)=1，递归体（确定递归求解时的递归关系）是 fun(n)=n*fun(n-1)，n>1。

int fun(int n){
    if(n==1)
        return 1;
    else
        return n*fun(n-1);
   }

----------------------------
原文链接:https://blog.csdn.net/JiuZhang_ninechapter/article/details/104658730
作者：九章算法
程序猿的技术大观园：www.javathinker.net

[这个贴子最后由 flybird 在 2020-03-08 22:51:19 重新编辑]

Java精品书籍推荐