|
|
PageRank 算法原理
PageRank 的计算充分利用了两个假设: 数量假设和 质量假设。步骤如下:
1 )在初始阶段:网页通过链接关系构建起Web 图,每个页面设置相同的PageRank 值,通过若干轮的计算,会得到每个页面所获得的最终PageRank 值。随着每一轮的计算进行,网页当前的PageRank 值会不断得到更新。
2 )在一轮中更新页面PageRank 得分的计算方法:在一轮更新页面PageRank 得分的计算中,每个页面将其当前的PageRank 值平均分配到本页面包含的出链上,这样每个链接即获得了相应的权值。而每个页面将所有指向本页面的入链所传入的权值求和,即可得到新的PageRank 得分。当每个页面都获得了更新后的PageRank 值,就完成了一轮PageRank 计算。
( 常言道,看一个人怎样,看他有什么朋友就知道了。也就是说,一个人有着越多牛X 朋友的人,他是牛X 的概率就越大。将这个知识迁移到网页上就是“ 被越多优质的网页所指的网页,它是优质的概率就越大” 。
PageRank 的核心思想就是上述简单却有效的观点。)
PageRank 算法 优缺点
优点:
是一个与查询无关的静态算法,所有网页的PageRank 值通过 离线计算获得;有效减少在线查询时的计算量,极大 降低了查询响应时间。
缺点:- 人们的查询具有主题特征,PageRank 忽略了主题相关性 ,导致结果的相关性 和主题性降低
- 旧的页面等级会比新页面高 。因为即使是非常好的新页面也不会有很多上游链接,除非它是某个站点的子站点。
- 该算法在初期的时候一直都是基于链接分析的, 而一个网页上的链接包含很多: 比如广告链接、功能链接、导航链接、以及多次重复的无效链接等等, 这些链接都会被该算法计算在pr 值传递之中, 所以 不能够对网页降噪之后在进行处理
基本思想 :
如果网页T 存在一个指向网页A 的连接,则表明T 的所有者认为A 比较重要,从而把T 的一部分重要性得分赋予A 。这个重要性得分值为:PR (T )/ L(T)
其中PR (T )为T 的PageRank 值,L(T) 为T 的出链数
则A 的PageRank 值为一系列类似于T 的页面重要性得分值的累加。
即一个页面的得票数由所有链向它的页面的重要性来决定,到一个页面的 超链接 相当于对该页投一票。一个页面的PageRank 是由所有链向它的页面(链入页面)的重要性经过 递归 算法得到的。一个有较多链入的页面会有较高的等级,相反如果一个页面没有任何链入页面,那么它没有等级。
3.3 PageRank 简单计算:
假设一个由只有4 个页面组成的集合:A ,B ,C 和D 。如果所有页面都链向A ,那么A 的PR (PageRank )值将是B ,C 及D 的和。
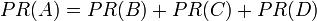
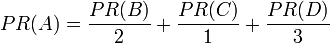
继续假设B 也有链接到C ,并且D 也有链接到包括A 的3 个页面。一个页面不能投票2 次。所以B 给每个页面半票。以同样的逻辑,D 投出的票只有三分之一算到了A 的PageRank 上。
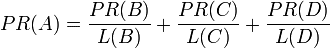
换句话说,根据链出总数平分一个页面的PR 值。
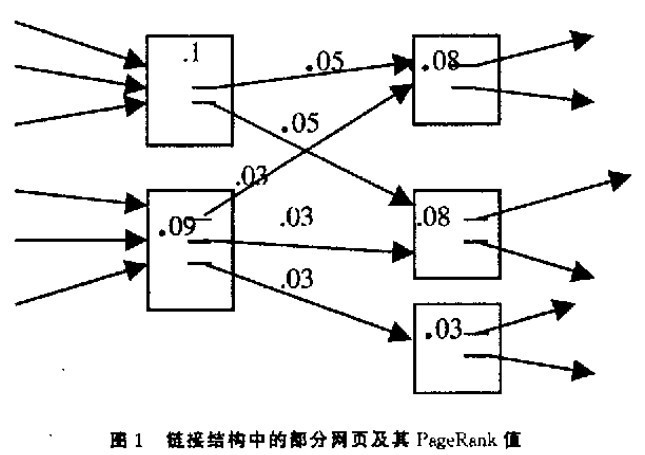
如图1 所示的例子来说明PageRank 的具体计算过程。
修正PageRank 计算公式 :
由于存在一些出链为0 ,也就是那些不链接任何其他网页的网, 也称为孤立网页,使得很多网页能被访问到。因此需要对 PageRank 公式进行修正,即在简单公式的基础上增加了 阻尼系数(dampingfactor )q , q 一般取值q=0.85 。
其意义是,在任意时刻,用户到达某页面后并继续向后浏览的概率。 1- q= 0.15 就是用户停止点击,随机跳到新URL 的概率)的算法被用到了所有页面上,估算页面可能被上网者放入书签的概率。
>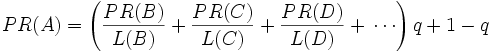
最后,即所有这些被换算为一个百分比再乘上一个系数q 。由于下面的算法, 没有页面的 PageRank 会是0 。所以,Google 通过数学系统给了每个页面一个最小值。
所以一个页面的PageRank 是由其他页面的PageRank 计算得到。Google 不断的重复计算每个页面的PageRank 。如果给每个页面一个随机PageRank 值(非0 ),那么经过不断的重复计算,这些页面的 PR 值会趋向于正常和稳定 。这就是搜索引擎使用它的原因。
( 一个很显然的结论是,如果连通图中有一个顶点的入度为 0 ,则经过有限次迭代之后,该连通图内的所有顶点的 PageRank 均为 0 ,形象的说,这个顶点就像一个黑洞一样,把整体的 PageRank 值慢慢地“吸收”了。由于它不对外贡献任何 PR 值,所以整体的 PR 总和是在不断地减少,直到最终收敛到 0 。我把它称之为: PageRank 的“黑洞效应”。至于说 Google 是如何防止这种情况的发生,毕竟一个网站没有外链是完全有可能的,我也尚未找到确切的答案。不过网上道是有人给出了一种解决办法:即如果一个网站没有外链,那么就假定该连通图内其余所有的网点都是它的外链,这样我们就避免了整体 PageRank 值被吸收的现象)
PageRank 幂法计算( 线性代数应用)
完整公式:
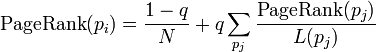
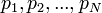 是被研究的页面, 是被研究的页面,
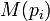 是 是
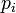 链入页面的数量, 链入页面的数量,
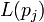 是 是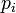 链出页面的数量,而N 是所有页面的数量。 链出页面的数量,而N 是所有页面的数量。
PageRank 值是一个特殊矩阵中的特征向量。这个特征向量为:
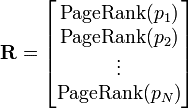
R 是如下等式的一个解:
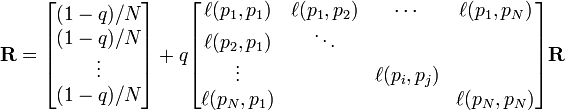
如果网页i 有指向网页j 的一个链接,则
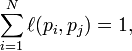 否则 否则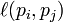 =0 。 =0 。
4.2 使用幂法求PageRank
PageRank 公式可以转换为求解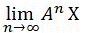 的值, 的值,
其中矩阵为 A = q*P + (1-q) * e 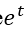 /N 。 P 为概率转移矩阵,e /N 。 P 为概率转移矩阵,e 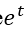 为 n 维的全 1 行. 则 e 为 n 维的全 1 行. 则 e 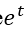 = =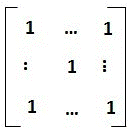
幂法计算过程如下:
X 设任意一个初始向量, 即设置初始每个网页的 PageRank 值均。一般为1.
R = AX;
while (1 )(
if ( l X - R I < ε ) { // 如果最后两次的结果近似或者相同,返回R
returnR;
} else {
X =R;
R = AX;
}
}
求解步骤:
一、 P 概率转移矩阵的计算过程:
先建立一个网页间的链接关系的模型, 即我们需要合适的数据结构表示页面间的连接关系。
1) 首先我们使用图的形式来表述网页之间关系:
现在假设只有四张网页集合:A 、B 、C ,其抽象结构如下图1 :
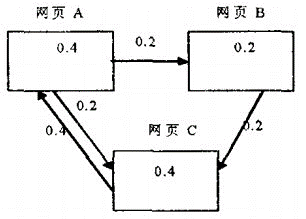
图1 网页间的链接关系
显然这个图是强连通的(从任一节点出发都可以到达另外任何一个节点)。
2 )我们用矩阵表示连通图:
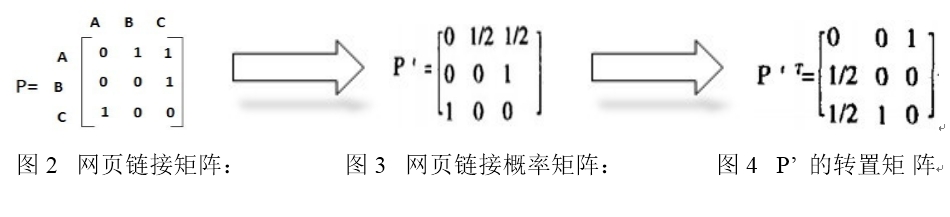
用邻接矩阵 P 表示这个图中顶点关系 ,如果顶(页面)i 向顶点(页面)j 有链接情况 ,则Pij = 1 ,否则 Pij = 0 。如图2 所示。如果网页文件总数为N ,那么这个网页链接矩阵就是一个N*N 的矩阵 。
3 )网页链接概率矩阵
然后将每一行除以该行非零数字之和,即(每行非0 数之和就是链接网个数)则得到新矩阵P’ ,如图3 所示。 这个矩阵记录了 每个网页跳转到其他网页的概率,即其中i 行j 列的值表示用户从页面i 转到页面j 的概率。图1 中A 页面链向B 、C ,所以一个用户从A 跳转到B 、C 的概率各为1/2 。
4 )概率转移矩阵P
采用P’ 的转置矩 阵进行计算, 也就是上面提到的概率转移矩阵P 。 如图4 所示:
二、 A 矩阵计算过程。
1 )P 概率转移矩阵 :
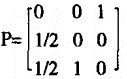
2 ) e 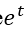 /N 为: /N 为:
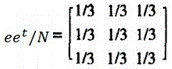
3 )A 矩阵为:q × P + ( 1 一 q) * e
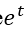 /N= 0.85 × P + 0.15 * e /N= 0.85 × P + 0.15 * e 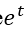 /N /N

初始每个网页的 PageRank 值均为1 , 即X~t = ( 1 , 1 , 1 ) 。
三、 循环迭代计算PageRank 的过程
第一步:
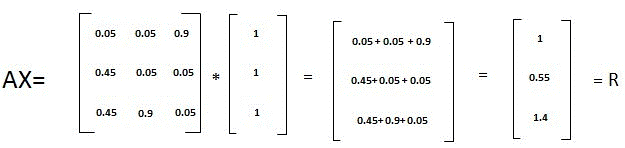
因为X 与R 的差别较大。 继续迭代。
第二步:
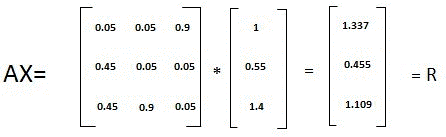
继续迭代这个过程...
直到最后两次的结果近似或者相同,即 R 最终收敛 ,R 约等于X ,此时计算停止。最终的R 就是各个页面的 PageRank 值。
用幂法计算PageRank 值总是收敛的,即计算的次数是有限的。
不论初始值如何选取,这种算法都保证了网页排名的估计值能收敛到他们的真实值。
由于互联网上网页的数量是巨大的,上面提到的二维矩阵从理论上讲有网页数目平方之多个元素。如果我们假定有十亿个网页,那么这个矩阵 就有一百亿亿个元素。这样大的 矩阵相乘,计算量是非常大的。Larry Page 和Sergey Brin 两人利用 稀疏矩阵计算的技巧,大大的简化了计算量。
----------------------------
原文链接:https://blog.51cto.com/9492221/1564068
程序猿的技术大观园:www.javathinker.net
[这个贴子最后由 flybird 在 2020-03-16 11:14:01 重新编辑]
|
|

















